자연상수 e는 무한히 이어지는 성장과 변화를 표현하는 수학의 핵심 상수입니다. e의 역사, 발견 배경, 그리고 오늘날 과학과 금융에서 왜 중요한지 알아봅니다.
📜 e의 탄생 — 로그와 복리에서 시작된 이야기
자연상수 e(≈ 2.71828)는 우리가 익숙한 원주율 π처럼, 인류가 오랜 세월에 걸쳐 ‘발견’한 수학적 진리입니다. 이 상수의 기원은 17세기 스코틀랜드의 수학자 존 네이피어(John Napier)가 로그(logarithm)를 고안하면서 시작되었습니다. 그의 로그는 계산을 단순하게 만들었지만, 시간이 지나면서 자연로그(natural logarithm)로 발전하며 e가 중심이 됩니다. 한편, 스위스 수학자 야코프 베르누이(Jacob Bernoulli)는 복리이자(Compound Interest) 문제를 연구하면서 e를 다시 발견했습니다. 그는 1의 이자율로 1년간 복리로 불어나는 금액을 계산하다가 다음 식을 얻게 됩니다:
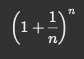
이 값을 n이 무한히 커질 때 극한을 취하면 2.71828…이 나오며, 바로 이것이 자연상수 e의 정의입니다.


🔬 왜 ‘자연’ 상수일까?
“자연상수”라는 이름은 자연현상에 가장 자주 등장하는 상수이기 때문입니다. 성장, 감쇠, 확률, 통계, 미적분 등 거의 모든 변화의 수학적 모델에서 e가 자연스럽게 나타납니다.
예를 들어:
- 세균이 증식하거나 방사능이 감소할 때
- 은행의 이자가 매 순간 복리로 계산될 때
- 기계 학습에서 손실함수를 미분할 때
- 확률분포(정규분포, 포아송분포 등)를 계산할 때
모두 e의 거듭제곱이 등장합니다. 즉, 자연의 변화율을 가장 잘 표현하는 수가 바로 e인 것입니다.
🧠 미적분학에서의 e — 변화의 언어
미적분에서 e는 특별한 의미를 가집니다. 함수 f(x) = e^x의 미분은 다시 자기 자신입니다.

이 말은 e^x는 변해도 본질이 변하지 않는 유일한 함수라는 뜻입니다. 이 때문에 e는 ‘변화의 본질’을 이해하는 핵심 도구가 되었고, 뉴턴과 라이프니츠의 미적분학 발전에 결정적인 역할을 했습니다.
💰 금융과 경제에서의 e — 복리의 마법
금융에서도 e는 매순간 불어나는 돈의 원리를 설명합니다. 예를 들어, 1년 이자율이 100%인 예금에 매 순간 복리로 이자를 붙인다면, 원금은 정확히 e배가 됩니다.
즉, 1원이 1년 후 2.71828원이 되는 셈입니다.
현대 금융에서는 이 개념이 지속적인 성장률, 물가 상승률, 할인율 계산, 옵션 가격 모델(블랙-숄즈 방정식) 등에 널리 활용됩니다.
🌌 수학 그 이상의 존재 — e의 철학적 의미
π가 ‘공간의 질서’를 상징한다면, e는 ‘시간과 변화의 본질’을 상징한다고 할 수 있습니다. 우주와 생명, 그리고 인간의 사고까지 — 모든 것은 시간에 따라 변합니다. e는 바로 그 변화의 속도, 성장의 리듬, 소멸의 패턴을 수식으로 표현하는 수학적 언어입니다.
🧩 정리 — e가 중요한 이유
| 분야 | e의 역할 |
| 수학 | 로그, 미분, 적분의 핵심 상수 |
| 금융 | 복리이자, 성장률, 할인율 계산 |
| 과학 | 자연현상의 성장·감쇠 모델링 |
| 통계 | 정규분포, 확률밀도함수의 기반 |
| 철학 | 변화와 균형의 상징 |
✨ 마무리 — 세상의 모든 변화 속에 있는 e
e는 단순한 숫자가 아닙니다. 그것은 자연의 리듬, 시간의 언어, 그리고 수학의 심장박동입니다. 우리의 삶이 끊임없이 성장하고 변화하는 한, e는 언제나 그 속에 존재합니다.
'재밌는 Tech.' 카테고리의 다른 글
| 🧠 인공지능의 진화 한번에 정리 (전통적 AI → 생성형 AI → AGI → ASI) (0) | 2025.11.24 |
|---|---|
| 👨🔬 라그랑주(Lagrange)는 도대체 뭐길래 맨날 나오지? 라그랑주 점? (0) | 2025.11.22 |
| 🌟 LangChain이 뭐야? 쉽게 이해하기: AI 개발의 핵심 도구 (0) | 2025.10.21 |
| 💻 big endian과 little endian의 차이와 이해하기 쉽게 풀어보기 (0) | 2025.09.05 |
| ₿ 코인 하드포크 vs 소프트포크: 비트코인 사례로 알아보는 안전성 🔐 (4) | 2025.08.13 |



